데이터를 특정 항목을 기준으로 정렬하고 싶을 수 있습니다.
퀵 정렬 알고리즘과 같은 방법으로 정렬을 할 수 있겠지만 정렬에는 비용이 발생합니다.
또 정렬된 자료구조에서 데이터의 변경이 발생하는 경우 변경 때마다 정렬된 상태를 지키기 위해서 정렬 비용을 계속해서 지불해야만 합니다.
삽입과 삭제가 빠르면서도 정렬이 되어있는 자료구조가 있다면 어떨까요?
놀랍게도 그러한 자료구조가 존재합니다.
그게 바로 오늘 포스팅할 "트리"입니다.
1. 트리 (Tree)란?
트리는 노드 기반 자료 구조이면서 구성 요소인 각 노드는 여러 노드로의 링크를 포함할 수 있습니다.
그 모습이 마치 나무를 연상시킨다 하여 트리라 명명하였습니다.
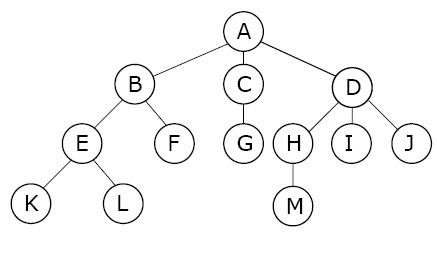
2. 트리의 고유 용어
트리 자료구조에는 트리에서만 사용하는 고유 용어가 존재합니다.
- 가장 상위 노드를 루트 (root)라 부릅니다.
- 특정 노드의 바로 위에 위치하는 상위 노드를 부모 (Parent), 바로 아래 위치하는 하위 노드를 자식 (Child)이라 부릅니다.
- 특정 노드를 생겨나게 한 모든 노드를 조상 (Ancestor), 특정 노드로부터 생겨난 모든 노드를 자손 (descendant)이라 부릅니다.
- 트리에는 레벨 (Level)이 존재하며, 각 레벨은 트리에서 같은 줄입니다.
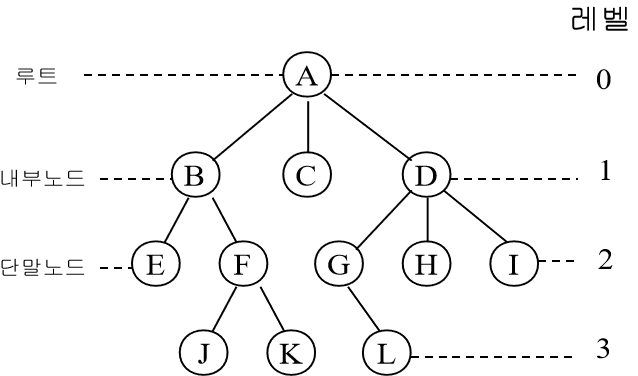
- 트리의 프로퍼티는 균형 잡힌 정도를 뜻하며 모든 노드에서 하위 트리의 노드 개수가 같으면 그 트리는 균형 트리입니다.
3. 이진 탐색 트리 ( Binary Search Tree )
트리 기반 자료 구조는 다양하지만 이번 포스팅에서는 이진 탐색 트리에 대해 이야기 해 보겠습니다.
이진 탐색 트리는 다음과 같은 규칙을 가지고 있습니다.
- 각 노드의 자식은 최대 왼쪽에 하나, 오른쪽에 하나 존재할 수 있습니다.
- 한 노드의 왼쪽 자손은 그 노드보다 작은 값만 포함할 수 있으며 오른쪽 자손은 그 노드보다 큰 값만 포함할 수 있습니다.
코드로는 다음과 같이 구현할 수 있습니다.
class BinaryTreeNode {
data;
leftChild;
rightChild;
constructor(data, leftChild = null, rightChild = null) {
this.data = data;
this.leftChild = leftChild;
this.rightChild = rightChild;
}
}
4. 이진 탐색 트리의 검색
이번엔 이진 탐색 트리의 자료 구조 연산 중 검색에 대해 알아보겠습니다.
검색은 다음과 같이 진행됩니다.
- 검사할 노드를 현재 노드로 지정합니다. ( 시작은 루트 노드 )
- 현재 노드의 값을 확인합니다.
- 찾고 있는 값 일시에는 현재 노드를 반환합니다.
- 찾고 있는 값이 현재 노드보다 작으면 왼쪽 하위 트리를 차례로 검색합니다.
- 찾고 있는 값이 현재 노드보다 크면 오른쪽 하위 트리를 차례로 검색합니다.
- 찾고 있는 값을 찾거나 트리의 바닥 ( 자식이 더 이상 존재하지 않는 경우 ) 도달 시까지 1 ~ 5 단계를 반복합니다.
코드로 구현해 보겠습니다.
search(searchValue, node) {
// 기저 조건 : 바닥에 도달하거나 찾고자 하는 값을 찾은 경우
if (node === null || node.data === searchValue) {
return node;
// 현재 노드 값이 찾고자 하는 값보다 작은 경우 왼쪽 자식 방향으로 검색
} else if (node.data < searchValue) {
return search(searchValue, node.leftChild)
// 현재 노드 값이 찾고자 하는 값보다 큰 경우 오른쪽 자식 방향으로 검색
} else {
return search(searchValue, node.rightChild)
}
}찾고자 하는 범위가 절반씩 줄어나가기 때문에 시간 복잡도는 $ O(logN) $ 이 나오게 됩니다.
5. 이진 탐색 트리의 삽입
이진 탐색 트리는 삽입에서 여타 자료구조들과 비교하였을 때 굉장히 뛰어납니다.
검색과 같이 차례로 비교해 가며 아래 방향으로 내려갑니다.
더 이상 내려갈 노드가 없을 때에 해당 노드의 값보다 작다면 왼쪽 위치, 크다면 오른쪽 위치에 노드를 삽입해 주면 됩니다.
검색 - $ logN $ 단계 + 삽입 - $ 1 $단계 가 필요하기 때문에 시간 복잡도는 $ O(logN) $이 됩니다.
코드로 구현해 보겠습니다.
function insert(data, node) {
// 삽입하고자 하는 데이터가 현재 노드 데이터 보다 작은 경우
if (data < node.data) {
// 왼쪽 자식 위치가 비어있다면 해당 위치로 삽입
if (node.leftChild === null) {
node.leftChild = new Node(data, null, null)
} else {
// 왼쪽 자식 위치에 노드가 존재 한다면 왼쪽 자식 따라 이동
insert(data, node.leftChild)
}
// 삽입하고자 하는 데이터가 현재 노드 데이터 보다 큰 경우
} else if (data > node.data) {
// 오른쪽 자식 위치가 비어있다면 해당 위치로 삽입
if (node.rightChild === null) {
node.rightChild = new Node(data, null, null)
} else {
// 오른쪽 자식 위치에 노드가 존재 한다면 오른쪽 자식 따라 이동
insert(data, node.rightChild)
}
}
}
트리는 같은 값의 원소들이라 할지라도 삽입되는 순서에 따라 다른 형태의 트리가 만들어지게 됩니다.
정렬된 입력 순서일수록 불균형한 트리가 생성되고 성능은 떨어지게 됩니다.
6. 이진 탐색 트리의 삭제
삭제는 이진탐색 트리에서 가장 어려운 연산이며 주의 깊게 실행해야 합니다.
다음과 같은 규칙이 있습니다,
- 삭제할 노드의 자식이 없다면 노드를 바로 삭제합니다.
- 삭제할 노드의 자식이 하나면 노드를 삭제하고 자식을 삭제한 노드가 있던 위치에 넣습니다.
- 자식이 둘인 노드를 삭제할 때는 삭제된 노드를 후속자 노드 (successor)로 교체합니다. 후속자 노드란 삭제된 노드보다 큰 값 중 최솟값을 갖는 자식노드입니다.
- 후속자 노드를 찾으려면 삭제된 값의 오른쪽 자식을 방문해서 그 자식의 왼쪽 자식을 따라 계속 방문해서 더 이상 왼쪽 자식이 없을 때까지 내려갑니다. 바닥 값이 후속자 노드입니다,
- 만일 후속자 노드의 오른쪽 자식이 있으면 후속자 노드를 삭제된 노드가 있던 자리에 넣은 후 후속자 노드의 오른쪽 자식을 후속자 노드의 원래 부모의 왼쪽 자식으로 넣습니다.
꽤 많은 규칙이 존재합니다.
코드로 구현해 보겠습니다.
function deleteNode(valueToDelete, node) {
// 트리 바닥에 도달한 경우 기저 조건
if (node === null) {
return null
}
// 삭제하려는 값이 현재 노드보다 크거나 작으면
// 현재 노드의 왼쪽 혹은 오른쪽 하위 트리에 대한 재귀 호출의 반환 값을
// 각각 왼쪽 혹은 오른쪽 자식에 할당
// ( 실제 자식 노드들이 자기 자신을 반환 하는 경우가 다수 )
else if (valueToDelete < node.data) {
node.leftChild = deleteNode(valueToDelete, node.leftChild)
return node
} else if (valueToDelete > node.data) {
node.rightChild = deleteNode(valueToDelete, node.rightChild)
}
// 현재 노드가 삭제 하려는 노드인 경우
else if (valueToDelete === node.data) {
// 현재 노드에 한쪽 자식이 없는 경우 해당 노드를 상위 노드의 자식으로 반환
// 하여 현재 노드 삭제
if (node.leftChild === null) {
return node.rightChild
} else if (node.rightChild === null) {
return node.leftChild
}
// 현재 노드에 자식이 둘 존재하는 경우 후속자 노드의 값으로 바꿈
// lift 함수 호출로 현재 노드 삭제
else {
node.rightChild = lift(node.rightChild, node)
return node
}
}
}
// 1. 후속자 노드를 찾는다
// 2. nodeToDelete 값을 후속자 노드로 덮어쓴다. 후속자 노드 객체를 옮기는 것이 아닌 그 값을 삭제중인 노드에 복사
// 3. 실제 후속자 노드 객체를 삭제하기 위해 원래 후속자 노드의 오른쪽 자식을 후속자 노드의 부모의 왼쪽 자식으로 넣는다.
// 4. 재귀가 모두 끝나면 처음에 전달 받은 rightchild를 반환하거나 원래 rightChild에 왼쪽 자식이 없어 원래
// rigthChild가 후속자 노드가 되었으면 null을 반환한다.
function lift(node, nodeToDelete) {
// 현재 노드에 왼쪽 자식이 있으면
// 왼쪽 하위 트리로 계속해서 내려가도록 재귀호출하여
// 후속자 노드를 찾는다
if (node.leftChild !== null) {
node.leftChild = lift(node.leftChild, nodeToDelete)
return node
}
// 현재 노드의 왼쪽 자식이 없는 경우
// 이 함수의 현재 노드가 후속자 노드라는 뜻이므로
// 현재 노드의 값을 삭제하려는 노드의 새로운 값으로 할당한다
else {
nodeToDelete.data = node.data
// 후속자 노드의 오른쪽 자식이 부모의 왼쪽 자식으로 쓰일수 있게 반환한다.
return node.rightChild
}
삭제 연산의 시간 복잡도 또한 $ O(logN) $입니다.
7. 이진 탐색 트리의 순회
이진 탐색 트리를 정렬된 순서대로 출력하고자 한다면 어떻게 해야 할까요?
먼저 트리의 모든 노드를 빠짐없이 방문해야 합니다.
자료 구조에서 모든 노드를 방문하는 과정을 순회 (traversal)라 부릅니다.
둘째로 리스트를 순서대로 출력할 수 있도록 해야 합니다.
이 포스트에서는 중위 순회 (inorder traversal)라 알려진 방법을 오름차순으로 수행하겠습니다.
중위 순회는 다음과 같은 순서로 진행됩니다.
- 노드의 왼쪽 자식에 함수를 재귀적으로 호출합니다.
- 현재 노드를 방문합니다.
- 노드의 오른쪽 자식에 함수를 재귀적으로 호출합니다.
코드로는 다음과 같이 구현할 수 있습니다.
traverseAndPrint(node){
if(node === null) return
this.traverseAndPrint(node.leftChild)
console.log(node.data)
this.traverseAndPrint(node.rightChild)
}
마치며
트리는 다른 자료구조보다 연산 과정이 복잡하고 규칙이 많은 만큼 뛰어난 효율성을 발휘합니다.
이진 탐색 트리 이외에도 다른 형태의 특수한 상황에서 뛰어난 효율성을 발휘하는 트리들이 존재합니다.
다음 포스트들에서 추가로 소개할 수 있도록 하겠습니다.
감사합니다.
'Computer Science > 자료구조' 카테고리의 다른 글
| 트라이 : 텍스트 데이터 특화 트리 (0) | 2023.03.27 |
|---|---|
| 힙과 우선순위 큐 : 제일 큰 값, 작은 값 (0) | 2023.03.25 |
| 연결리스트 : 대량 삽입과 삭제에 유리한 Node 기반 자료구조 (0) | 2023.03.18 |
| 스택과 큐 - 제약을 통한 문제 해결 전략 (0) | 2023.03.11 |
| 해시 테이블 - 빠른 검색 (0) | 2023.03.11 |
