이번 포스트에서는 거품정렬 ( Bubble Sort )에 대해서 알아보도록 하겠습니다.
거품정렬에는 곧 소개할 기본형 외에 파생된 방식들이 존재하지만 이번에는 오름차순 기본 정렬 형태를
알아보도록 하겠습니다.
시작하겠습니다.
1. 거품 정렬 ( Bubble Sort ) 이란?
거품 정렬 이름의 유래는 정렬하는 방식을 선으로 이었을 때 마치 거품이 올라오는 모습을 닮았다 하여
이름이 붙여졌다고 합니다.

정렬 방식은 서로 인접한 두 원소를 비교하여 크기가 순서대로 ( 여기서는 오름차 순 ) 되어 있지 않다면 교환해줍니다.
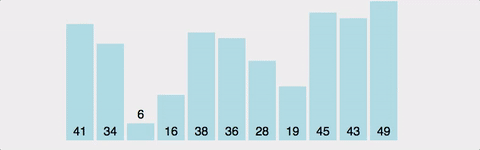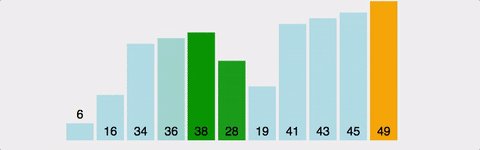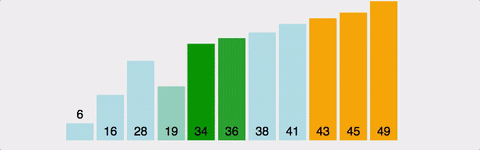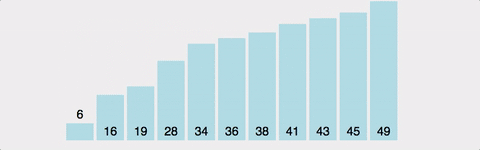
2. 거품 정렬의 진행
첫 패스스루에서는
첫 번째 원소와 두 번째 원소를 비교,
두번째 원소와 세 번째 원소를 비교,
세번째 원소와 네 번째 원소를 비교,
...
최종적으로는 ( N -1 )과 N 번째 원소를 비교하며 각 단계에서 주어진 조건 ( 여기서는 뒤에 위치한 원소가 크다 )에 부합하지 않으면 원소를 교환합니다.
이렇게 첫 패스스루가 끝나면 배열 내 가장 큰 원소는 가장 뒤에 위치하게 됩니다.
때문에 다음 패스스루부터는 정렬이 끝난 가장 뒤의 원소는 제외하고 다시 첫 패스스루와 같은 방식으로 진행합니다.
이렇게 패스스루를 반복해서 수행하면 제외되는 데이터가 패스스루마다 하나씩 늘어나고 최종적으로 배열이 정렬된 채로 종료됩니다.
3. 거품 정렬의 코드 구현
function bubbleSort(arr) {
// i : 패스스루
for (let i = 0; i < arr.length; i++) {
// j : 비교할 두 원소 중 뒤에 위치할 원소의 인덱스
for (let j = 1; j < arr.length - i; j++) {
// 앞에 위치한 원소가 더 크다면 인접한 해당 원소들 교환
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}4. 거품 정렬의 효율성
- 시간 복잡도
1번째 패스스루에서 N−1단계
2번째 패스스루에서 N−2단계
....
마지막 패스스루에서 1단계로
(N−1)+(N−2)+...+1=N(N−1)/2
O(N(N−1)/2) = O(N2) 가 나오게 됩니다.
- 공간 복잡도
주어진 공간 내에서 교환을 통해 정렬되므로 O(N)입니다.
5. 거품정렬의 장단점
- 장점
* 구현이 단순하고 직관적
* 자료 구조 내에서만 교환이 이루어져 별도 메모리 사용 없음 => 제자리 정렬
* 중복된 값인 경우에도 입력 순서로 정렬 보장 => 안정 정렬
- 단점
* 시간 복잡도 상대적 비효율적
* 잦은 교환 연산의 발생
마치며
이번 포스팅에서는 버블 정렬에 대해서 알아보았습니다.
버블 정렬 알고리즘은 정렬 알고리즘 중 굉장히 비효율적인 알고리즘입니다.
실제로 사용되는 경우가 드물지만 입사 면접 질문이나 손코딩으로 출제 및 제시가 되기 때문에 알아두어야
하는 알고리즘입니다.
참고자료
'알고리즘-이론' 카테고리의 다른 글
| 삽입 정렬 - 여기 말고 저기 빈 자리 가서 앉으세요 (0) | 2023.03.08 |
|---|---|
| 선택 정렬 - 자리를 얻기 위한 경쟁 (0) | 2023.03.08 |
| Big-O Notation - 시간 복잡도 (0) | 2023.03.07 |
| 이진 탐색 - 간단하고 강력한 탐색 알고리즘 ( 2 ) (1) | 2023.03.04 |
| 이진 탐색 - 간단하고 강력한 탐색 알고리즘 ( 1 ) (0) | 2023.03.04 |
